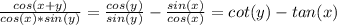Question

Prove: cos(x+y)/cosxsiny=coty-tanx

Answer 1

cos (x+y)/cos x sin y

= cos x cos y - sin x sin y / cos x sin y

= cos x cos y/cos x sin y - sin x sin y / cos x sin y

hope this helps

Answer 2

Use Cosine Sum identity

Explanation:

It's a simple demonstration if you know what trigonometric identity you should use. In this case use cosine sum identity which states:

`cos(a+b)=cos(a)*cos(b)-sin(a)*sin(b)`

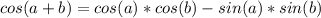
Also keep in mind this property of fractions:

`(a \pm b)/(c) =(a)/(c) \pm (b)/(c) \hspace{3} c\\eq0`

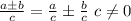
Using the previous information:

`(cos(x+y))/(cos(x)*sin(y))=(cos(x)*cos(y)-sin(x)*sin(y))/(cos(x)*sin(y))=(cos(x)*cos(y))/(cos(x)*sin(y))-(sin(x)sin(y))/(cos(x)*sin(y))\\    \\=(cos(y))/(sin(y)) -(sin(x))/(cos(x))`

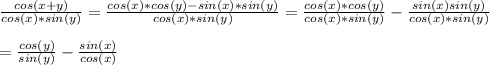
Also, according to the basic identities:

`(cos(\theta))/(sin(\theta)) =cot(\theta)\\\\(sin(\theta))/(cos(\theta))= tan(\theta)`

Therefore:

`(cos(x+y))/(cos(x)*sin(y))=(cos(y))/(sin(y)) -(sin(x))/(cos(x))=cot(y)-tan(x)`