Question

[8.06] Which polynomial is a perfect square trinomial?

49x2 − 28x + 16

4a2 − 20a + 25

25b2 − 20b − 16

16x2 − 24x − 9

Answer 1

4a² − 20a + 25.    is the answer.     

Answer 2

Answer:
`4a^2 - 20a + 25`

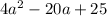
Explanation:

A binomial
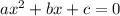`ax^2+bx+c=0` is called perfect square trinomial

if
`b^2 = 4ac` is satisfied.

For
`49x^2 - 28x + 16`

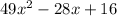
a = 49, b = -28 and c = 16,

`(-28)^2=784`

`4* 49* 16 =3136`

`\implies (-28)^2\\eq 4(49)(16)`

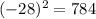
Thus,
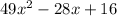`49x^2 - 28x + 16` is not a perfect square trinomial.

For
`4a^2 - 20a + 25`

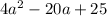
a = 4, b = -20 and c = 25,

`(-20)^2=400`

`4* 4* 25 =400`

`\implies (-20)^2\\eq 4(4)(25)`

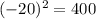
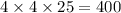
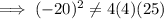
Thus,
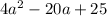`4a^2 - 20a + 25` is a perfect square trinomial.

For
`25b^2 - 20b - 16`

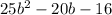
a = 25, b = -20 and c = -16,

`(-20)^2=400`

`4* 25* 16 =-1600`

`\implies (-20)^2\\eq 4(25)(16)`

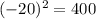
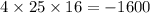
Thus,
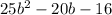`25b^2 - 20b - 16` is not a perfect square trinomial.

For
`16x^2 - 24x - 9`

a = 16, b = -24 and c = -9,

`(-24)^2=576`

`4* 16* -9 =-576`

`\implies (-24)^2\\eq 4(16)(-9)`

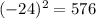
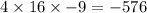
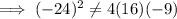
Thus,
`16x^2 - 24x - 9` is not a perfect square trinomial.