Question

The width of a square-based storage tank is 3m less than its height. The tank has a capacity of 20 m3. If the dimensions are integer values in metres, what are they?

Answer 1

Let the dimensions of the tank be x by x by (x + 3)
Volume = x(x)(x + 3) = x^3 + 3x^2 = 20
x^3 + 3x^2 - 20 = 0
x = 2

Therefore, the dimension of the tank is 2 m by 2 m by 5 m

Answer 2

The answer is h = 5 m, w = 2 m

The volume of a rectangle is: V = w * l * h (w - width, l - length, h - height)
A rectangle is square based, so: w = l
V = w * w * h = w² * h

The width of a square-based storage tank is 3m less than its height: w = h - 3
V = 20 m³

w² * h = 20
(h - 3)² * h = 20
(h² - 2 * h * 3 + 3²) * h = 20
(h² - 6h + 9) * h = 20
h² * h - 6h * h + 9 * h = 20
h³ - 6h² + 9h = 20
h³ - 6h² + 9h - 20 = 0
h * h² - 5h² - h² + 5h + 4h - 4*5 =0
(h * h² - 5 * h²) - (h * h - 5h) + (4*h - 4*5) =0
h²(h - 5) - h(h - 5) + 4(h - 5) = 0
(h - 5)(h² - h + 4) = 0

We have that one solution is:
h - 5 = 0
h1 = 5

Other two solutions are:
h² - h + 4 = 0

Quadratic equation is: ax² + bx + c = 0

`h_(2,3) = \frac{-b+/- \sqrt{ b^(2)-4ac } }{2a} = \frac{-(-1)+/- \sqrt{ (-1)^(2)-4*1*4 } }{2*1} = (1+/- √(1-16) )/(2) = \\ \\ = (1+/- √(-15) )/(2) = (1+/- √(-1*15) )/(2) = (1+/- √(-1) * √(15) )/(2)= (1+/- i√(15) )/(2) \\ \\ h_2 = (1+ i√(15) )/(2) \\ \\ h_3 = (1- i√(15) )/(2)`

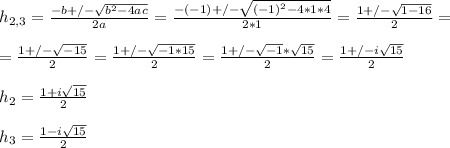
The only integer value is h1 = 5 m

h = 5 m
w = h - 3 = 5 - 3 = 2 m