Question

Engineering Physics

The x and y component of a vector is 3 and 5, respectively. What is the angle between the vector and positive x-axis?

Answer 1

The angle between the vector and positive x-axis is approximately 59.036º.

Step-by-step explanation:

By Linear Algebra and to be precise, by definition of Dot Product we can determine the angle between two vector from following expression:

`\theta = \cos^(-1)(\vec u \,\bullet \,\vec v)/(\|\vec u\|\cdot \|\vec v\|)` (1)

Where:

`\vec u`,
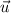`\vec v` - Vectors, no unit.

`\|\vec u\|`,
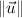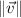`\|\vec v\|` - Norms of vectors, no unit.

`\theta` - Angle, measured in sexagesimal degrees.

Please notice that norms are calculated by Pythagorean Theorem. If we know that
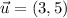`\vec u = (3,5)` and
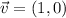`\vec v = (1, 0)`, then the angle between the vector and positive x-axis is:

`\|\vec u\| = \sqrt{3^(2)+5^(2)}`

`\|\vec u\| = √(34)`

`\|\vec v\| = 1`

`\theta = \cos^(-1)((3)\cdot (1)+(5)\cdot (0))/(√(34)\cdot 1 )`

`\theta = \cos^(-1)(3)/(√(34))`

`\theta \approx 59.036^(\circ)`

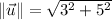
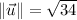
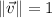
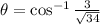
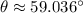
The angle between the vector and positive x-axis is approximately 59.036º.