information that we have
Width --> I will call the width "x"
Length ---> Since the length is 70 less than 3 times the width, that means the length is: "3x-70"
In summary:
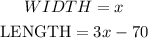
We know that the perimeter of the base is:
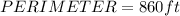
Next, we use the formula for perimeter, which is:
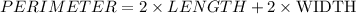
And we substitute the values that we have for perimeter, length and width:
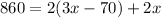
We need to solve this equation for x to be able to find the dimensions.
-Use distributive property to multiply 2 by 3x and by -70:
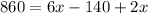
Combine like terms (the two terms with x on the right side):
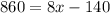
Add 140 to both sides of the equation:
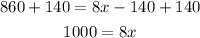
Next we divide both sides by 8: