Question

The ordered pairs (1, 6), (2, 36), (3, 216), (4, 1296), and (5, 7776) represent a function. What is a rule that represents this function?

Answer 1

From what I gathered the x-values are going up by plus 1(+1) and the y-value are going up by times 6(×6). Now that you have this find the formula/rule.

Answer 2

The rule is
`\\ f(x) = 6^(x)`

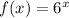
Explanation:

The resulting values are powers of 6:

`\\ 6^(1) = 1`

`\\ 6^(2) = 36`

`\\ 6^(3) = 216`

`\\ 6^(4) = 1296`

`\\ 6^(5) = 7776`

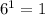
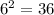
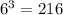
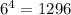
One factor that is not defined in the question is whether the domain (the set of values for which a function is defined [WolframAlpha, 2019]) of the function
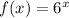`\\ f(x) = 6^(x)` is only for x = {1, 2, 3, 4, 5} or defined for all possible values this function can take, that is, x = (-∞;∞) or all real numbers.

As you can see from the graph attached:

• Theoretically, this function could take all values for x = (-∞;∞). If this were the case, the function is a continuous line with resulting values (that is, the range of the function) for f(x)>0 (0;∞). The graph below shows only positive values (x > 0) and values for x ≤ 5.

• For values x = {1, 2, 3, 4, 5}, the function is discrete (not a continuous line) and only defined for these values. In this case, the function would be represented only by the points in the graph, and the values it could take would be only f(x) = {6, 36, 216, 1296, 7776}, which would represent the range for this function.

In the last case, we have to redefine the function as:

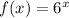`\\ f(x) = 6^(x)` for
`x = \{1, 2, 3, 4, 5\}`.