solve the equations
first one
take the sqrt of both sides
x-y=√71
add y to both sides
x=y+√71
sub y+√71 for x in other part
(y+√71)²+y²=59
y²+2y√71+71+y²=59
2y²+2y√71+71=59
minus 59 both sides
2y²+2y√71+12=0
factor out 2
2(y²+y√71+6)=0
use quadratic equation or something
y=
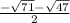
and
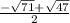
sub those for x
x=y+√71
note: √71=(2√71)/2
x=
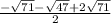
,
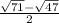
or
x=
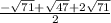
,
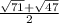
xy=
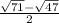
times
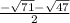
or
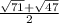
times
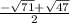
the result is -6 both times
xy=-6