Question

If f(x) = *#4, g(x)= x-2, and M(x) - 4x-1, what is (fonog)(x)?2x+16o (fon•g)(x) =хo (tong)(x) 2x+44x-3o (Fonog)(x) = 4x=1o (Fonog)(x) = 4x=94x-5

Answer 1

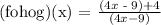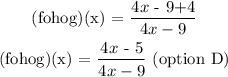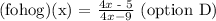
`(\text{fohog)(x) = }\frac{4x\text{ - }5}{4x-9}\text{ (option D)}`Step-by-step explanation:

(fohog)(x): we would replace the value of x in g(x) with the h(x) function.

Then the result we would replace with the x value in f(x) function

g(x) = x - 2

h(x) = 4x - 1

(hog)(x) = 4(x-2) -1

(hog)(x) = 4x - 8 - 1 = 4x - 9

we replace x in f(x) with the value we got in (hog)(x)

f(x) = (x+4)/x

`(\text{fohog)(x) = }\frac{(4x\text{ - 9)+4}}{(4x-9)}`
`\begin{gathered} (\text{fohog)(x) = }\frac{4x\text{ - 9+4}}{4x-9} \\ (\text{fohog)(x) = }\frac{4x\text{ - }5}{4x-9}\text{ (option D)} \end{gathered}`