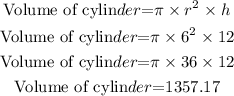Question

The first one I already did I just need help on the rest you can choose any radii it doesn't matter.

Answer 1

As given by the question,

There are given that the sphere and cylinder.

Now,

From the formula of volume of sphere and volume of a cylinder.

Then,

`\begin{gathered} \text{Volume of sphere=}(4)/(3)*\pi* r^3 \\ \text{Volume of cylin}der\text{=}\pi* r^(^2)* h \end{gathered}`

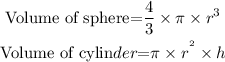
Now

Find the last two values of volume of a sphere

So,

For the volume of the sphere,

Let r be the 4cm and 6 cm.

So,

(2)

The second volume of the sphere is:

`\begin{gathered} \text{Volume of sphere=}(4)/(3)*\pi* r^3 \\ \text{Volume of sphere=}(4)/(3)*\pi*(4)^3 \\ \text{Volume of sphere=}(4)/(3)*\pi*64 \\ \text{Volume of sphere=268.08} \end{gathered}`

Then,

(3)

The third volume of the sphere is:

`\begin{gathered} \text{Volume of sphere=}(4)/(3)*\pi* r^3 \\ \text{Volume of sphere=}(4)/(3)*\pi*(6)^3 \\ \text{Volume of sphere=}(4)/(3)*\pi*216 \\ \text{Volume of sphere=}904.77 \end{gathered}`

Now,

To find the volume of the cylinder, first, find the height of the cylinder

Then,

According to the question, the height of the cylinder is equal to the diameter of the sphere.

That means, for the height of the cylinder find the diameter of the sphere

So,

From the diameter of sphere

`\text{diameter of sphere=}d=2r`

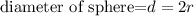
Then,

Put r=4 for second cylinder and r=6 for third cylinder

Then,

`\begin{gathered} \text{diameter of sphere=}d=2r \\ \text{diameter of sphere=}d=2(4) \\ \text{diameter of sphere=}d=8=h \end{gathered}`

And,

`\begin{gathered} \text{diameter of sphere=}d=2r \\ \text{diameter of sphere=}d=2(6) \\ \text{diameter of sphere=}d=12=h \end{gathered}`

Now,

Find the volume of a cylinder for second part:

So,

`\begin{gathered} \text{Volume of cylin}der\text{=}\pi* r^(^2)* h \\ \text{Volume of cylin}der\text{=}\pi*(4)^(^2)*8 \\ \text{Volume of cylin}der\text{=}\pi*16^{}^{}*8 \\ \text{Volume of cylin}der\text{=}402.12 \end{gathered}`

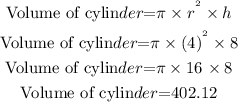
And,

For the third part:

`\begin{gathered} \text{Volume of cylin}der\text{=}\pi* r^2^{}* h \\ \text{Volume of cylin}der\text{=}\pi*6^2^{}*12 \\ \text{Volume of cylin}der\text{=}\pi*36*12 \\ \text{Volume of cylin}der\text{=}1357.17 \end{gathered}`