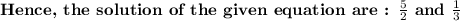Question

What are the solutions to the equation (2x – 5)(3x – 1) = 0?

Answer 1

`\textbf{The solution of the given equation are : }(5)/(2)\textbf{ and }(1)/(3)`

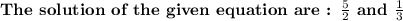
Step-by-step explanation:

The equation is given to be : (2x – 5)(3x – 1) = 0

We need to find the values of x such that the value of the equation is 0 and those corresponding values of x will be our required solution of the given equation.

Now, the product of two factors is given to be 0

⇒ Either of the two factors is equal to 0

So, first taking 2x - 5 = 0 and finding the value of x

⇒ 2x = 5

`\implies\bf x=(5)/(2)`

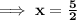
Now, taking the second factor equal to 0 and finding the other value of x

⇒ 3x - 1 = 0

⇒ 3x = 1

`\implies\bf x = (1)/(3)`

So, we get :

`\bf x =(5)/(2)\textbf{ and }x=(1)/(3)`

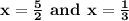
Hence, these two values of x are the required solution of the given equation

`\textbf{Hence, the solution of the given equation are : }(5)/(2)\textbf{ and }(1)/(3)`

Answer 2

Answer:
`x=(5)/(2), x=(1)/(3)`

Step-by-step explanation:

The equation is:

`(2x-5)(3x-1)=0`

The term on the left consists of a product of two different factors: therefore, this product can be zero if either the first term (2x-5) or the second term (3x-1) is equal to zero.

This means that we can solve separately for the two terms:

`2x-5=0\\3x-1=0`

Solving the first equation:

`2x-5=0\\2x=5\\x=(5)/(2)`

Solving the second equation:

`3x-1=0\\3x=1\\x=(1)/(3)`