Answer: Value of f(x)=32 when the value of x=8
Explanation:
Since we have given that
the function f(x) varies directly with x and f(x).
If x=40, f(x)=40
So, if x=8 then we have to find the value of f(x):
Since there is direct variation,
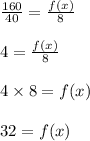
So, value of f(x)=32 when the value of x=8.