Question

A pole that is 3.1 m tall casts a shadow that is 1.16 m long. At the same time, a nearby building casts a shadow that is 46.25 m long. How tall is the building? Round your answer to the nearest meter.

Answer 1

`124\text{ m}`

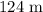
Step-by-step explanation:

Here, we want to get the height of the building

Firstly, we need a diagrammatic representation of the presented information

We have that as follows:

The structures and their shadows form right triangles

Right triangles are similar

When two shapes are similar, the ratio of their corresponding sides is equal

Thus, we have it that:

`\begin{gathered} (1.16)/(3.1)\text{ = }(46.25)/(h) \\ \\ h\text{ = }(46.25*3.1)/(1.16) \\ \\ h\text{ = 123.599 m} \end{gathered}`

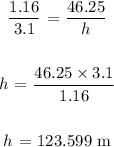
To the nearest m, this is 124 m