Question

A farmer plans to use 25 meters of fencing to enclose a rectangular pen that has an area 63 m^2. Only three sides of the pen need fencing because part of an existing wall will be used for one of the longer sides. Find the dimensions.

Answer 1

we have that

the area of the rectangular pen is equal to

A=L*W

A=63m2

so

L*W=63 ------> equation 1

the perimeter with 25 meters of fencing (Only three sides) is equal to

P=L+2W

L is the longer side

P=25

25=L+2W -----> L=25-2W -----> equation 2

substitute equation 2 in equation 1

(25-2W)*W=63

25W-2W^2=63

2w^2-25w+63=0

solve the quadratic equation using the formula

a=2

b=-25

c=63

substitute

`w=\frac{-(-25)\pm\sqrt[]{-25^2-4(2)(63)}}{2(2)}`

`w=(25\pm11)/(4)`

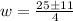
the values of w are

w=9 and w=3.5

Find out the value of L

For w=9 m

L=25-2(9)=7 m

is not the solution because L is the longer side

so

For w=3.5 m

L=25-2(3.5)=18 m

therefore

The dimensions are

Length 18 meters

Width 3.5 meters