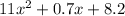Answer:
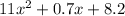
Explanation:
Given: A biologist studied the populations of white-sided jackrabbits and black-tailed jackrabbits over a 5-year period. The biologist modeled the populations, in thousands, with the following polynomials where x is time, in years.
white-sided jackrabbits:

black-tailed jackrabbits:

The polynomial models the total number of white-sided and black-tailed jackrabbits is given by :-
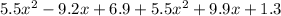
Combining like terms we get,
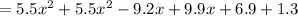
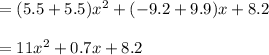
Hence, the polynomial models the total number of white-sided and black-tailed jackrabbits is