Question

A 920 kg block is pushed on the slope of a 30

frictionless inclined plane to give it an initial
speed of 50 cm/s along the slope when the block is 2.3 m from the bottom of the incline.
The acceleration of gravity is 9.8 m/s2 . What is the speed of the block at the bot-
tom of the plane?
Answer in units of m/s

Answer 1

using the kinetic energy theorem, we have:
sumW = 1/2 mV²final - 1/2mV²initial
sumW=mgh, where h=sin30 x AB, AB= 2.3m
50 cm/s=0.5m/s

so 2gsin30 AB = V²final - V²initial and V final = sqrt(2gsin30 AB + V²initial)

finally v= 4.77m/s

Answer 2

The mass of the block is 920 kg.

The angle of inclination of the slope with respect to the plane is 30 degree.

The initial speed of the block [u] =50 cm/s

=50×0.01 m/s

=0.5 m/s

The block is once pushed and it moves downward on the slope. The distance of the block from the bottom is 2.3 m .

Hence the distance travelled by the block [s]=2.3 m

We are asked to calculate the final velocity of the block when it touches the ground.

First we have to calculate the acceleration of the block.

Resolving g into horizontal and vertical component we get,

`[1] gsin\theta\ is\ along\ the\ slope\ and\ downward`

`[2] gcos\theta\ is\ along\ the\ normal\ drawn\ to\ the\ block`

Now putting the equation of kinematics we get-

`v^2=u^2+2as`

Here v is called final velocity and a is the acceleration.

`=[0.5]^2+2*gsin\theta *2.3`

`=0.25+2*gsin30*2.3`

`=0.25+[2*9.8*0.5*2.3]` [sin30=0.5]

`=22.79`

`v=√(22.79)\ m/s`

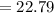
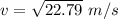
`v=4.78 m/s` [ans]