Question

L=8 w=4 h=2

Find the diagonal(d) of the base

Answer 1

Diagonal of base is 8.94 (approx)

Explanation:

Consider the given dimension

Length = 8 units

width = 4 units

and height = 2 units.

We have to find the diagonal (d) of the base.

Since the solid, having 3 sides length, breadth and height is a cuboid. So, its base must be a rectangle.

Also, base have dimension length and width.

So, Diagonal of base =
`\sqrt{\text{Length}^2+\text{width}^2`

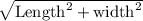
Substitute the values, we get,

Diagonal of base =
`\sqrt{{8}^2+{4}^2`

Diagonal of base =
`√(64+16)`

Diagonal of base =
`√(80)`

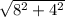
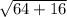
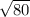
Diagonal of base = 8.94 (approx)

Thus, diagonal of base is 8.94 (approx)

Answer 2

length = 8
width = 4
height =2

The question is which base do you mean because there are 3 different bases. I assume you mean largest one which in this case is 8x4 base

Diagonal of it is:
d = sqrt(8^2 + 4^2) = sqrt(64+16) = sqrt(80) = sqrt(16*5) = 4*√5