Question

A rocket is launched from atop a 105-foot cliff with an initial velocity of 156 ft/s. The height of the rocket above the ground at time t is given by h = –16t2 + 156t + 105. When will the rocket hit the ground after it is launched? Round to the nearest tenth of a second.

4.9 s
9.8 s
0.6 s
10.4 s

Answer 1

h = –16t2 + 156t + 105, when t = t', the time where the rocket hit the ground after it is launched, so 105= –16t'2 + 156t' + 105, so -16t'2 + 156t' = 0 implies t' =0 or -16t'+ 156= 0, equivalent to t'=9.75, so the answer is
b) 9.8 s

Answer 2

The correct option is 4. The rocket will hit the ground after 10.4 s.

Explanation:

The given function is

`h=-16t^2+156t+105`

Where, h is height of the rocket above the ground at time t.

The rocket will hit the ground, when h=0.

`0=-16t^2+156t+105`

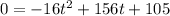
Using quadratic formula

`t=(-b\pm √(b^2-4ac))/(2a)`

`t=(-156\pm √((156^2-4(-16)(105)))/(2(-16))`

`t=-0.632,10.382`

The time can not negative, therefore after 10.382 second the rocket will hit the ground.

`10.382\approx 10.4`

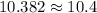
Therefore the correct option is 4. The rocket will hit the ground after 10.4 s.