Question

Find the area of an isosceles triangle with a vertex of 42 and a base of 6 inches

Answer 1

As given by the question

There are given that the vertex angle is 42 degrees and the base is 6 inches.

Now,

If the vertex angle of the isosceles triangle is 42 degrees, so each of the base angles is:

`\begin{gathered} (180-42)/(2)=(138)/(2) \\ =69 \end{gathered}`

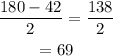
And,

The base of the triangle is 6 inches

So, the altitude of the triangle is:

`\begin{gathered} ((6)/(2))*\tan 69^(\circ)=3*\tan 69^(\circ) \\ =7.81\text{ inches} \end{gathered}`

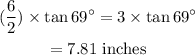
Then,

The area of the triangle is:

`\begin{gathered} \text{Area of triangle=}(6*7.81)/(2) \\ \text{Area of triangle}=23.43 \end{gathered}`

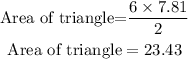
Hence, the area of the triangle is 23.43.