As given by the question
There are given that the vertex angle is 42 degrees and the base is 6 inches.
Now,
If the vertex angle of the isosceles triangle is 42 degrees, so each of the base angles is:
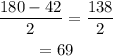
And,
The base of the triangle is 6 inches
So, the altitude of the triangle is:
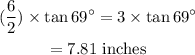
Then,
The area of the triangle is:
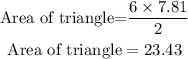
Hence, the area of the triangle is 23.43.