Question

If cos x = .75, what is sin x?

Answer 1

sin x = 0.66

Explanation:

Given : cos x = .75,

To find : what is sin x.

Solution : We have given cos x = .75

By the trigonometric identity : cos²x + sin²x = 1.

sin x =
`\sqrt{1-cos^(2)x }`.

Plug the values of cos x

sin x =
`\sqrt{1- (0.75)^(2) }`.

sinx =
`√(1- 0.5625)`.

sinx =
`√(0.4375)`.

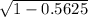sin x = 0.66

Therefore, sin x = 0.66

Answer 2

ArcCos (.75) = x = 41.409

plug the x value into sin x and solve it

You will find that sin x = 0.66

Hope this helps