Question

A = 40, c = 41, b =
1
9
57
81

Answer 1

`A = 40, c = 41, b = ? \\ \\ cos(\angle A)= (c)/(b) \\ \\ cos(40^o)= (41)/(b) \\ \\b=\frac{41} {cos{40^o}}= 53.5`

Answer 2

Option C is correct

the value of b approximately is, 57 units

Explanation:

Using Pythagoras theorem in a right angle triangle:

`\text{Hypotenuse side}^2=\text{Opposite side}^2+\text{Adjacent side}^2`

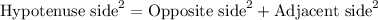
As per the statement:

In ACB,

a = 40 units , c = 41

Solve for b:

Using Pythagoras theorem;

`b^2=a^2+c^2`

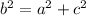
Substitute the given values we have;

`b^2 = 40^2+41^2`

⇒
`b^2 = 3281`

⇒
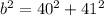
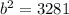
`b = √(3281) = 57.280014` units

Therefore, the value of b approximately is, 57 units