Answer:
The person died 51,788 years ago.
Step-by-step explanation:
Let the initial amount of carbon-14 in the body when person was alive =

Amount of carbon-14 left after t years =
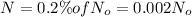
t = time elapsed
Decay constant of carbon-14=
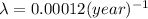
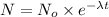
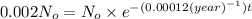
![\ln[0.002 N_o]=\ln[N_o]-{(0.00012 (year)^(-1))* t](https://img.qammunity.org/2017/formulas/chemistry/high-school/1h6snvwgvdvcyyusbe3xampgcezn6yaupi.png)
t = 51,788.40 years ≈ 51,788 years
Since the carbon-14 in less than 0.02 % in the body which means the person must have died 51,788 years ago.