We have to apply the log properties to expand this expression.
We start by writing the original equation:
![\log \lbrack(x^2+13x-90)^3\cdot\sqrt[5]{\frac{(x^2-9)^3}{(x+6)^{(3)/(4)}}}\rbrack](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/c1kxn40ry4uto7nhcpfi.png)
We start with the multiplication, converting the two factors in two logarithmic terms:
The product property is:
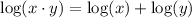
Then, applied to our equation becomes:
![\log \lbrack(x^2+13x-90)^3\cdot\sqrt[5]{\frac{(x^2-9)^3}{(x+6)^{(3)/(4)}}}\rbrack=\log \lbrack(x^2+13x-90)^3\rbrack+\log (\sqrt[5]{\frac{(x^2-9)^3}{(x+6)^{(3)/(4)}}})](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/7ce40b13zy2wjeatl155.png)
Then, we take the first term and applied the log of power rule:
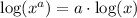
Then, if we apply this to the first term, we get:
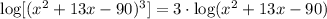
and for the second term:
![\log (\sqrt[5]{\frac{(x^2-9)^3}{(x+6)^{(3)/(4)}}})=\log \lbrack(\frac{(x^2-9)^3}{(x+6)^{(3)/(4)}})^{(1)/(5)}\rbrack=(1)/(5)\cdot\log (\frac{(x^2-9)^3}{(x+6)^{(3)/(4)}})](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/v958k8axct9e7xw32t1l.png)
With the first term we can no longer expand it as it is, as we have additions and substractions only. This can be changed by factorizing the quadratic equation: then we can express the quadratic equation as the product of two factors and apply the product rule.
We apply the quadratic formula to find the roots of the quadratic equation:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-13\pm\sqrt[]{13^2-4\cdot1\cdot(-90)}}{2\cdot1} \\ x=\frac{-13\pm\sqrt[]{169+360}}{2} \\ x=\frac{-13\pm\sqrt[]{529}}{2} \\ x=(-13\pm23)/(2) \\ x_1=(-13-23)/(2)=(-36)/(2)=-18 \\ x_2=(-13+23)/(2)=(10)/(2)=5 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/asounlayoe375rr1s1mb.png)
Now, we can express the first term as:
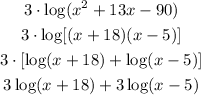
That is the first term fully expanded.
We now continue with the second term.
We start applying the quotient rule:
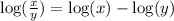
Then, our second term becomes:
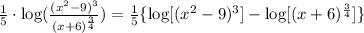
We then apply the log of power:
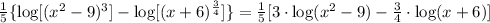
Finally, the term (x²-9), as it is a difference of squares, can be expressed as:
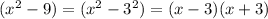
Now, as we have a product, we can apply the product rule:
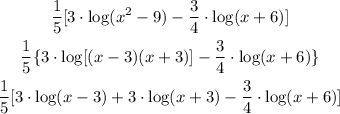
If we apply the distributive property we get:
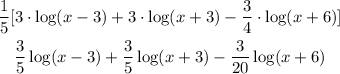
We now add the first and second term and get:
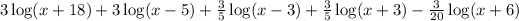
Answer: the equivalent expression expanded is
3*log(x+18) + 3*log(x-5)+3/5*log(x-3)+3/5*log(x+3)-3/20*log(x+6)