Question

Describe the relationship of the segments made when chords intersect inside a circle. Use the following image as reference.

Answer 1

Answer with explanation:

Following theorems are used when there are segments that is chords are drawn inside the circle

1. Equal chords are equidistant from the center.

2. Perpendicular from the center to the chord bisects the chord.

3. Chord which are larger in length is nearer from the center.

⇒If these two segments are equal in length

X +W=Z +Y

Otherwise, X+W > Z +Y

There is other relation possible between segment.

Join A, B,C and D.

In Δ AOB and ΔCOD

Angle in the same segment of a circle are equal.

→∠1=∠2

→∠3=∠4

→∠5=∠6------Vertically opposite angle

⇒ Δ AOB ≅ ΔCOD----[AAA similarity]

When triangles are similar their sides are proportional.

`\rightarrow (OA)/(OD)=(OB)/(OC)\\\\\rightarrow (X)/(Z)=(Y)/(W)`

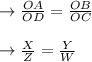
→X W=Z Y

Answer 2

there is a theorem that said that the ratio of lengths of chords at point of intersection are the same.
I think the relationship would be X/W = Y/Z

hope this helps