Question

Find the 7th term of a geometric sequence with t1 = 6 and r = 4.

Answer 1

24,576.

Explanation:

We have been given that first term of a geometric sequence is 6 and common ratio is 4. We are asked to find the 7th term of the sequence.

We know that a geometric sequence is in form
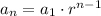`a_n=a_1\cdot r^(n-1)`, where,

`a_n` = nth term of sequence,

`a_1` = 1st term of sequence,

`r` = common ratio.

Upon substituting
`a_1=6` and
`r=4` and
`n=7` in geometric sequence formula, we will get:

`a_7=6\cdot(4)^(7-1)`

`a_7=6\cdot(4)^(6)`

`a_7=6\cdot 4,096`

`a_7=24,576`

Therefore, the 7th term of the given geometric sequence would be 24,576.

Answer 2

To solve for the 7th term of a geometric sequence with t1 = 6 and r = 4, we use the following equation:

a(n) = a(1) r^(n-1)
a7 = (6) 4^(7-1)
a7 = 24576

Hope this answers the question. Have a nice day. Feel free to ask more questions.