Question

Given the equation below, graph the polynomial by hand. On your graph indicate x and y intercepts, multiplicity and end behavior. If you have any questions about how to share this handwritten work please let your teacher know. h(x)=(x+3)^2(x-2)

Answer 1

We need to sketch the function:

`h\mleft(x\mright)=\mleft(x+3\mright)^2\mleft(x-2\mright)`

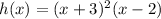
We say that a zero xₙ of a polynomial p(x) has multiplicity n, if we can write the polynomial as:

`(x-x_n)^n\cdot q(x)`

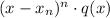
Thus, we see that h(x) has the zeros:

• -3, with multiplicity 2

• 2, with multiplicity 1

Also, this polynomial function has degree 3 (the major degree of x in the polynomial).

And has a positive leading coefficient (the coefficient of x³ is 1).

Then, since this polynomial function has an odd degree and a positive leading coefficient, its end behavior is:

`\begin{gathered} h(x)\rightarrow-\infty,\text{ as }x\rightarrow-\infty \\ \\ h(x)\rightarrow+\infty,\text{ as }x\rightarrow+\infty \end{gathered}`

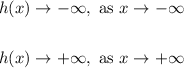
Therefore, the graph of h(x) grows from -∞ , touches the point (-3,0), decreases, then increases crossing the point (2,0):