We need to sketch the function:

We say that a zero xₙ of a polynomial p(x) has multiplicity n, if we can write the polynomial as:
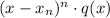
Thus, we see that h(x) has the zeros:
• -3, with multiplicity 2
• 2, with multiplicity 1
Also, this polynomial function has degree 3 (the major degree of x in the polynomial).
And has a positive leading coefficient (the coefficient of x³ is 1).
Then, since this polynomial function has an odd degree and a positive leading coefficient, its end behavior is:
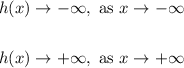
Therefore, the graph of h(x) grows from -∞ , touches the point (-3,0), decreases, then increases crossing the point (2,0):