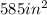Question

29.

Find the area of a regular hexagon with an apothem 13 inches long and a side 15 inches long. Round your answer to the nearest tenth.

585 in2
389.7 in2
97.4 in2
1,169.1 in2

Answer 1

Option 1st is correct

585
`\text{in}^2`

Explanation:

Area(A) of a regular hexagon is given by:

`A = (1)/(2)P \cdot a` ....[1]

where,

P is the perimeter and a is the apothem of the regular hexagon.

As per the statement:

An apothem 13 inches long and a side 15 inches long.

⇒a = 13 inches and side = 15 inches

Perimeter of hexagon(P) = 6s ; where s is the side

⇒P = 6(15) = 90 inches

Substitute the given values in [1] we have;

`A = (1)/(2) \cdot 90 \cdot 13`

Simplify:

A = 585 square inches.

Therefore, the area of a regular hexagon with an apothem 13 inches long and a side 15 inches long is,
`585 in^2`

Answer 2

An apothem is a line drawn from the centerpoint of the polygon to one side of the polygon. There is a formula for area in terms of apothem:

A = (1/2)*(Perimeter)*(Apothem)

The perimeter of the regular hexagon is just the length of one side multiplied with the number of sides. Since a hexagon has 6 sides,

P = 6(15) = 90in

A = 1/2 * 90 * 13
A = 585 square inches