Question

Find the perimeter of triangle CDE. Round to the nearest tenth.

(1 point)
90.0
18.0
14.3
10.5

Answer 1

Answer: 18.0

Explanation:

The distance formula to find the distance between two points P(a,b) and Q(c,d) is :_

`d=√((d-b)^2+(c-a)^2)`

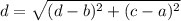
From the graph, the coordinates of ΔCDE are C(-3,1) , D(1,4) and E(3,-2).

Then, length of CD :-

`CD=√((4-1)^2+(1-(-3))^2)\\=√(9+16)=√(25)=5`

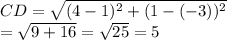
Length of DE :-

`DE=√((-2-4)^2+(3-1)^2)=√(36+4)\\=√(40)=5\approx6.3`

Length of EC :-

`EC=√((-3-3)^2+(1-(-2))^2)=√((-6)^2+(3)^2)\\=√(45)=5\approx6.7`

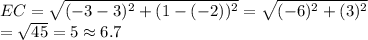
Now, the perimeter of triangle :_

`CD+DE+EC=5+6.3+6.7=18.0\text{ units}`

Hence, the perimeter = 18.0 units

Answer 2

Here's how you do it: you find all the distances between the three points and add them together to calculate the perimeter of the triangle. To calculate for the distance between two points, the formula is

d = √[(x2 - x1)² + (y2 - y1)²]

So, just take two points, assign x1 and x2 with corresponding y1 and y2, then you get the answer.

Points: D(1,4), E(3,-2), C(-3,1)

After substituting the answers would be:
DE = 6.3 units
CE = 6.7 units
CD = 5 units

Perimeter = 6.3 + 6.7 + 5
Perimeter = 18 units