Question

can u please answer the question because I've been having technical issue where it's been kicking me out.of the tutoring session

Answer 1

`\begin{gathered} \text{Similarity Criteria = AA} \\ m\measuredangle B=60\text{ degrees} \\ m\measuredangle F=60\text{ degrees} \\ AC=18 \\ BC=18 \\ DE=21 \\ DF=21 \end{gathered}`

Step-by-step explanation:

Given the figures in the attached image.

we want to prove that two triangles are similar.

We can observe that there are two equal corresponding angles in the triangle.

Therefore, we can use the AA similarity criteria. (AA - Angle Angle).

we can also calculate the remaining angles using the rule of "sum of angles in a triangle".

- Sum of angles in a triangle equals 180 degrees.

`\begin{gathered} m\measuredangle B=180^(\circ)-(60^(\circ)+60^(\circ)) \\ m\measuredangle B=180^(\circ)-120^(\circ) \\ m\measuredangle B=60^(\circ) \end{gathered}`
`\begin{gathered} m\measuredangle F=180^(\circ)-(60^(\circ)+60^(\circ)) \\ m\measuredangle F=180^(\circ)-120^(\circ) \\ m\measuredangle F=60^(\circ) \end{gathered}`

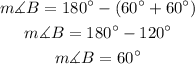
From the calculated angles, we can confirm that the three angles in each triangle are equal and equal to 60 degrees. So, the two triangles are Equilateral triangles and all sides of each triangle are equal.

So;

`\begin{gathered} AB=AC=BC=18 \\ \text{and} \\ DE=DF=EF=21 \\ \\ AC=18 \\ BC=18 \\ DE=21 \\ DF=21 \end{gathered}`

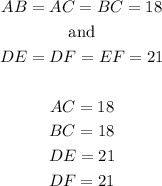
Therefore, we have;

`\begin{gathered} \text{Similarity Criteria = AA} \\ m\measuredangle B=60\text{ degrees} \\ m\measuredangle F=60\text{ degrees} \\ AC=18 \\ BC=18 \\ DE=21 \\ DF=21 \end{gathered}`