Question

In a random sample of 60 dog owners enrolled in obedience training, it was determined that the mean amount of money spent per owner was $109.33 per class. Assuming the population standard deviation of the amount spent per owner is $12, construct and interpret a 95% confidence interval for the mean amount spent per owner for an obedience class. Round your answer to the nearest hundreth.We are 95% confident that the mean amount spent per dog owner for a single obedience class is between ________ and ________.

Answer 1

In statistics, a confidence interval is a range of values that is determined through the use of observed data, calculated at the desired confidence level that may contain the true value of the parameter being studied.

The formula to calculate the confidence interval of a sample data is given to be:

`CI=\bar{x}\pm z(s)/(√(n))`

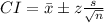
where:

CI = confidence interval

x = sample mean

z = confidence level value

s = sample standard deviation

n = sample size

From the question, we have the following parameters provided:

`\begin{gathered} \bar{x}=109.33 \\ s=12 \\ n=60 \end{gathered}`

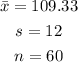
The z-score for a 95% confidence level is gotten to be 1.96.

Therefore, we can calculate the interval to be:

`\begin{gathered} CI=109.33\pm1.96*\frac{12}{\sqrt[]{60}} \\ CI=109.33\pm3.04 \end{gathered}`

Therefore the interval is between:

`\begin{gathered} \Rightarrow109.33+3.04=112.37 \\ \text{and} \\ \Rightarrow109.33-3.04=106.29 \end{gathered}`

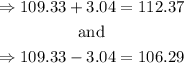
Hence, we are 95% confident that the mean amount spent per dog owner for a single obedience class is between $106.29 and $112.37.