Question

The width of a rectangle is fixed at 6cm. Determine (in terms of an inequality) those lengths for which the area will be less than 126cm^2

Answer 1

Step-by-step explanation:

The width is 6 cm, but the other dimension is unknown, that will be ''X''.

So, the area of the rectangle would be according to the expression:

`A = x . 6 (cm)`

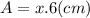
They want us to find a range of lengths with an area minor than
`126 cm^(2)`

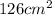
Therefore, this is an inequality problem, which expression will be:

`x . 6 < 126\\x < (126)/(6)\\ Hence, x < 21\\`

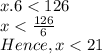
Finally, the length's range that ensure an area less than 126, it's all length less than 21.

Answer 2

126 cm^2 = 6cm * x

X = 126/6

= 21 cm

so, 21 is the highest value, which make the inequality be :

x ≤ 21