Step-by-step explanation:
For car Z, according to the Newton equation,
v = u + at
where, v = final velocity = 0
u = initial velocity = 120 km/h
a = acceleration
t = time = 4.2 hours
Putting the given values into the above formula as follows.
v = u + at
0 =

a = 28.571
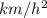
Also, it is known that
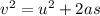
s =
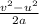
Putting the values into the above formula calculate for 's' as follows.
s =
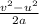
=
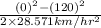
= 252.0 km
Since, 45 L of fuel is used by the car to travel 252 km. Then calculate car traveled km per liter as follows.
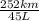
= 5.6 km/L
For car Q, v = u + at
0 =
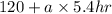
a =
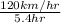
= 22.22
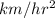
Now, calculate value of 's' for car Q as follows.
s =
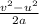
=

= 324.0 km
Hence, average kilometers traveled for liter of gas is as follows.
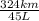
7.2 km/L
Thus, we can conclude that the average kilometers traveled for each liter of gas (km/L) by car Z is 5.6 km/L and for car Q is 7.2 km/L.