Question

Tan^2x +5tanx +3=0

Approximate to four decimal places the solutions for x,
0 less than or equal to x<2pi

Answer 1

The given equation is

`tan^(2)(x)+5tan(x)+3=0`

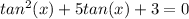
Where
`0\leq x\leq 2 \pi`, this interval means that we need to find the solution of the equation in every quadrant, remember that trigonometric equations are periodical, that means its solution repeats in other quadrants.

First, we need to make a variable change where
`y=tan(x)` and
`y^(2)=tan^(2)(x)`, so the equation is

`y^(2)+5y+3=0`

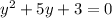
Now, we can solve the equation as a quadratic equation.

We know this equation has two solutions

`y^(2)+5y+3=(y+a)(y+b)`

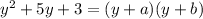
To find these solutions, we use the quadratic formula

`y_(1,2)=\frac{-2 (+-)\sqrt{b^(2) -4ac} }{2a}`

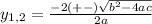
Where
`a=1, b=5, c=3`

Replacing these values, we have

`y_(1,2)=\frac{-5 (+-)\sqrt{5^(2) -4(1)(3)} }{2(1)}=(-5(+-)√(25-12) )/(2)\\ y_(1,2)=(-5(+-)√(13) )/(2)=(-5(+-)3.6)/(2)`

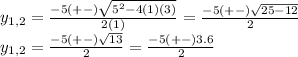
So,

`y_(1)=(-5+3.6)/(2)=-0.7\\ y_(2)=(-5-3.6)/(2)=-4.3`

But,
`y=tan(x)`, so

`tan(x)=-0.7\\x=tan^(-1)(-0.7) \approx -35\\\\tan(x)=-4.3\\x=tan^(-1)(-4.3) \approx -77`

Answer 2

Tan^2 x + 5tan x + 3 = 0
Let tan x = m, then
m^2 + 5m + 3 = 0
m^2 + 5m + 25/4 = -3 + 25/4 = 13/4
(m + 5/2)^2 = 13/4
m + 5/2 = + or - sqrt(13) / 2
m = (√13 - 5)/2 or (-√13 - 5)/2

tan x = (√13 - 5)/2 or (-√13 - 5)/2
x = arctan((√13 - 5)/2) or arctan((-√13 - 5)/2)
x = 103.0837, 145.1149, 283.0837, 325.1149