Question

Find the remainder when f(x) is divided by (x - k)

f(x) = 3x3 - 4x2 - 3x + 14; k= 3

A. 50

B. 68

C. -12

D. 112

Answer 1

Simplify the function with the value of k and you will get the remainder.
f(x) = 3x3 - 4x2 - 3x + 14

f(3)=3×(3)^3−4×(3)^2−3×(3)+14

Simplify the above equation and that is your answer.

Answer 2

50

Explanation:

Find the remainder when f(x) is divided by (x - k)

`f(x) = 3x^3 - 4x^2 - 3x + 14`

To find the remainder , we use remainder theorem

Given that : k=3, Lets plug in 3 for x in f(x) and find f(3)

`f(x) = 3x^3 - 4x^2 - 3x + 14`

`f(3) = 3(3)^3 - 4(3)^2 - 3(3) + 14=50`

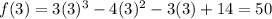
The remainder is 50

The remainder is 50 when f(x) is divided by (x-3)