Question

What is the sum of the geometric sequence 1, 3, 9, … if there are 12 terms?

292,524

265,720

139,968

104,976

Answer 1

The sum of the given geometric series if there are 12 terms is:

265,720

Explanation:

We are given a geometric sequence as:

1,3,9,.....

This means that the common ratio(r) of the sequence is: 3

Since each term is increasing by a multiple of '3'

Also, sum of an finite geometric series with n terms is given by:

`S_n=a* ((r^n-1)/(r-1))`

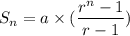
where n is the number of terms whose sum is calculated and a is the first term of the sequence.

We have n=12, a=1 and r=3

Hence, the sum is:

`S_(12)=1* ((3^(12)-1)/(3-1))\\\\\\S_(12)=(531440)/(2)\\\\\\S_(12)=265720`

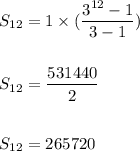
Hence, the sum is: 265,720

Answer 2

The sum of this geometric sequence is 265, 720.
1 + 3 + 9 + 27 + 81 + 243 + 729 + 2187 + 6561 + 19683 + 59049 + 177147 = 265, 720
You just multiply each number by 3 to find the sequence and then add those numbers.