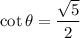Question

An acute angle θ is in a right triangle with sin θ =2/3 . What is the value of cot θ?

I found that 2 is the opposite angle and 3 is the hypotenuse.

adj/opp = cot θ, so adj/2 = cot θ

I tried using the Pythagorean Theorem, but I can get an answer choice! Please help! Thanks!

Answer 1

The value of cot θ is:

`\cot \theta=(√(5))/(2)`

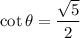
Explanation:

We are given:

`\sin \theta=(2)/(3)`

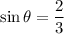
We know that the sine trignometric function is the ratio of the perpendicular to hypotenuse of the triangle corresponding to θ.

i.e. Perpendicular=2 units

and Hypotenuse = 3 units

We know that in a right angled triangle with leg lengths as a, b and hypotenuse c the Pythagorean Theorem says that:

`c^2=a^2+b^2\\\\\\3^2=2^2+b^2\\\\\\9=4+b^2\\\\\\b^2=5\\\\\\b=√(5)`

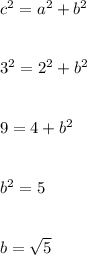
This means we get Base=√5 units

Also, we know that:

`\cot \theta=(base)/(Perpendicular)`

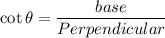
Hence, we get:

`\cot \theta=(√(5))/(2)`

Answer 2

The adjacent side can be found by the Pythagorean Theorem
a^2 + b^2 = c^2
x^2 + 2^2 = 3^2
x^2 + 4 = 9
x^2 = 9-4
x^2 = 5
x = sqrt(5)
So the adjacent side is sqrt(5) units
which means
cot(theta) = adj/opp
cot(theta) = sqrt(5)/2