Question

Find b and c so that (5,b,c) is orthogonal to both (1,2,3) and (1,-2,1)

Answer 1

Answer: The answer is 3.75 and -2.5.

Step-by-step explanation: We are given to find the values of b and c if the vector (5, b, c) is orthogonal to (1, 2, 3) and (1, -2, 1).

We know that if two vectors are orthogonal, then their dot product is equal to zero. So, we have

`(5, b, c).(1,2,3)=0\\\\\Rightarrow 5+2b+3c=0\\\\\Rightarrow 2b+3c=-5,~~~~~~~~~~~~~~~~~~~~(A)`

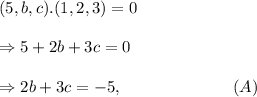
and

`(5,b,c).(1,-2,1)=0\\\\\Rightarrow 5-2b+c=0\\\\\Rightarrow -2b+c=-5.~~~~~~~~~~~~~~~~~~~~~(B)`

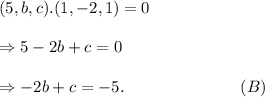
Adding equations (A) and (B), we have

`3c+c=-5-5\\\\\Rightarrow 4c=-10\\\\\Rightarrow c=-2.5,`

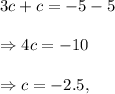
and from (B), we have

`-2b+2.5=-5\\\\\Rightarrow -2b=-7.5\\\\\Rightarrow b=3.75.`

Thus, the value of b is 3.75 and the value of c is -2.5.

Answer 2

{5+2b+3c=0
5−2b+c=0
adding both equations u get10+4c=0⇒c=−10/4=−5/2
then5−2b+(−5/2)=0⇒b=(5/2−5)/(−2)=5/2−5/4=5/4