Question

Two separate bacteria populations grow each month and are represented by the functions f(x) = 3x and g(x) = 7x + 6. In what month is the f(x) population greater than the g(x) population? Month 1 Month 2 Month 3 Month 4

Answer 1

one month = 13
2 months = 20

Answer 2

The answer is Never.

Explanation:

In order to determine the month, we have to graph both functions and then we have to determine the intercept point
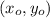`(x_o,y_o)` of the functions. With this information, for any "x" value greater than
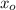`x_o`, one of both function will be greater that the other.

I have attached an image that shows the graph of both functions, where:

Red line:
`f(x)=3*x`

Blue line:
`g(x)=7*x+6`

As we see in the image, the intercept happens in the negative range of "x". Also we can see that the population of g(x) is always greater than f(x) for
`x>0`.

Therefore, never the f(x) population will be greater than g(x) population.