Question

A firecracker shoots up from a hill 140 feet high with an initial speed of 100 feet per second. Using the formula H(t) = −16t2 + vt + s, approximately how long will it take the firecracker to hit the ground?

5 seconds

7 seconds

9 seconds

11 seconds

Answer 1

7 seconds

Explanation:

A firecracker shoots up from a hill 140 feet high with an initial speed of 100 feet per second. Using the formula H(t) = −16t^2 + vt + s

v is the initial speed and s is the initial height

Initial speed v= 100 and initial height = 140

So the equation becomes H(t) = −16t^2 + 100t + 140

When the firecracket hit the ground the height becomes 0

So we plug in H(t) for 0 and solve for t

`0 = -16t^2 + 100t + 140`

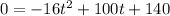
Apply quadratic formula

`x=(-b+-√(b^2-4ac))/(2a)`

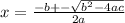
a= -16, b= 100, c= 140

`t=(-100+-√(100^2-4(-16)(140)))/(2(-16))`

`t=(-100+-√(18960))/(-32)`

`t=\frac{-100+-\4sqrt{1185}}{-32}`

`t=(25+-√(1185))/(8)`

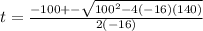
t=-1.18 or t= 7.43

it take 7 seconds for the firecracker to hit the ground

Answer 2

H(t) = -16t^2 + vt + s
0 = -16t^2 + 100t + 140
4t^2 - 25t - 35 = 0
t = 7 seconds.