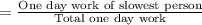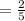Question

One person can do a certain job in ten minutes, and another person can do the same job in fifteen minutes. How many minutes will they take to do the job together?

If x represents how many minutes to do the job together, then how much of the job does the slowest person do?

Answer 1

One person can do the job in 10 minutes

So he can do 1/10th of the job in 1 minute

Similarly another person can do 1/15th of the job in 1 minute

Together they can do in 1 minute = 1/10 +1/15 = 5/30 = 1/6th of the job

So together they can finish the job in 6 minutes. ANSWER

slowest person does x/ 15 th of the job ANSWER

1/6 +1/2 +1/3 = 7/6

together they can do the job in 6/7 days

Answer 2

They will take 6 minutes to do the job together.

Slowest person do 2/5 of the total work.

Explanation:

Given,

Time taken by first person = 10 minutes,

⇒ One day work of the first person =
`(1)/(10)`,

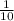While, time taken by second person = 15 minutes,

⇒ One day work of second person =
`(1)/(15)`,

So, when both persons work together, total one day work =
`(1)/(10)+(1)/(15)`,

`=(3+2)/(30)`

`=(5)/(30)=(1)/(6)`

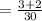
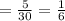
Thus, the total time taken by the both persons when they work together,

x =
`(1)/((1)/(6))` = 6 minutes

The one who takes more time is slower.

Now, the part of the work done by the slowest person ( second one),

`=\frac{\text{One day work of slowest person}}{\text{Total one day work}}`

`=(1/15)/(1/6)`

`=(2)/(5)`