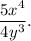Question

What is the simplified form of 15x^8/24y^5 divided by 4x^4/8y^2

Answer 1

(24y^5)/(15x^8) * 4x^4/(8y²)

Reduce the common factors for the numerator and denominator and multiply the fractions altogether to get...

24/8 * y^(5 - 2) * 4/15 * 1/x^(8 - 4)
= 3y³ * 4/15 * 1/x^4
= 4y³/(5x^4)

I hope this helps!

Answer 2

Answer: The required simplified form is
`(5x^4)/(4y^3).`

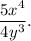
Step-by-step explanation: We are given to find he simplified form of the following division :

`(15x^8)/(24y^5)~~~\textup{divided by}~~~(4x^4)/(8y^2).`

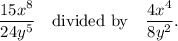
We know the following method :

`(a)/(b)/ (c)/(d)=(a)/(b)*(d)/(c).`

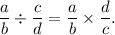
Also, we note the following rule of exponents :

`(x^a)/(x^b)=x^(a-b).`

The simplification of the given division is as follows :

`(15x^8)/(24y^5)~~~\textup{divided by}~~~(4x^4)/(8y^2)\\\\\\=(15x^8)/(24y^5)/ (4x^4)/(8y^2)\\\\\\=(15x^8)/(24y^5)*(8y^2)/(4x^4)\\\\\\=(5*2)/(8)*(x^(8-4))/(y^(5-2))\\\\\\=(5x^4)/(4y^3).`

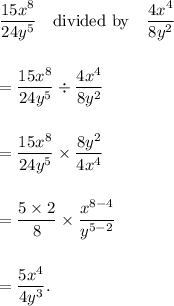
Thus, the required simplified form is
`(5x^4)/(4y^3).`