Question

Find the area of the regular hexagon.

Find the coordinates of the center. (x,y)


Find the base using the Pythagorean theorem, (round to the hundredth).


Find the height using the distance formula, (round to the hundredth).


Round your final answer to the nearest tenth

Answer 1

1) The area of the regular hexagon is approximately 11.256 unit²

2) The coordinates of the center is (2, 3)

3) The base length is approximately 2.08 units

4) The height of the hexagon is approximately 3.61 units

Explanation:

1) The length, lₐ, of the apothem is given as follows;

`l_a = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

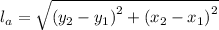
Therefore, for the apothem having coordinates, (2, 3), and (3, 1.5), we have;

`l_a = \sqrt{\left (3-1.5 \right )^(2)+\left (2-3 \right )^(2)} = √(1.5^2 + (-1)^2) =√(3.25)`

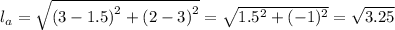
The length of half half of one side, S/2 = a × tan(30°) = √(3.25)/√3

The length of the base = 2 × √(3.25)/√3 ≈ 2.082 units

The perimeter, P = 6 × 2× √(3.25)/√3

The area, A = 1/2 × P × a = 1/2 × 6 × 2 × √(3.25)/√3 × √3.25 = (13·√3)/2

A = (13·√3)/2 unit²

The area of the regular hexagon, A = (13·√3)/2 unit² ≈ 11.256 unit²

2) The coordinates of the center = (2, 3)

3) The base, 'b', length by Pythagorean theorem is given as follows;

b = √(a² + (S/2)²) = √((√(3.25))² + (√(3.25)/√3)²) = √(3.25 + 3.25/3) = √(13/3) = (√39)/3

The base length, b = (√39)/3 units ≈ 2.08 units

4) The height of the hexagon, h = 2 × The length of the apothem, lₐ

The length, lₐ, of the apothem is given as follows;

`l_a = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

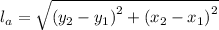
Given the apothem coordinates, (2, 3), and (3, 1.5), we have;

`l_a = \sqrt{\left (3-1.5 \right )^(2)+\left (2-3 \right )^(2)} = √(1.5^2 + (-1)^2) =√(3.25)`

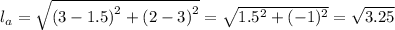
The height of the hexagon, h = 2 × √3.25 units ≈ 3.61 units.