Question

Given below are the coordinates of the vertices of a triangle. Find the lengths of the sides of the triangle, then click to identify the triangle as scalene, isosceles, or equilateral.

P(0, 0), Q(6, 0), R(3, 3rad3 )

Answer 1

Answer: ΔPQR is an equilateral triangle.

Step-by-step explanation: The vertices of a triangle PQR are given as follows:

P(0, 0), Q(6, 0) and R(3, 3√3).

We are to find the type of the triangle by finding the lengths of its three sides.

The lengths of the three sides PQ, QR and PR are calculated using distance formula as follows:

`PQ=√((6-0)^2+(0-0)^2)=√(36+0)=√(36)=6,\\\\QR=√((3-6)^2+(3\sqrt3-0)^2)=√(9+27)=√(36)=6,\\\\PR=√((0-3)^2+(0-3\sqrt3)^2)=√(9+27)=√(36)=6.`

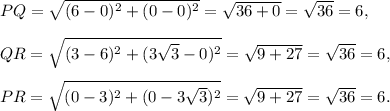
Therefore, PQ = QR = PR.

All the sides of the triangle PQR are equal, and so the triangle is equilateral.

Thus, ΔPQR is an equilateral triangle.