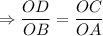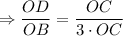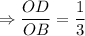Question

The figure below shows a trapezoid, ABCD, having side AB parallel to side DC. The diagonals AC and BD intersect at point O.

If the length of AO is three times the length of CO, the length of BO is

one-third the length of AC

one-third the length of AB

three times the length of DO

three times the length of DC

Answer 1

BO is the same length as AO, and DO is the same length as CO. therefore BO is three times the length of DO.

Answer 2

Length of BO is three times the length of DO.

Explanation:

In trapezoid ABCD,
`CD\ ||\ AB`

In ΔCDO and ΔABO,

1. 
   `m\angle CDO=m\angle ABO` (Alternate interior angles)
2. 
   `m\angle DCO=m\angle BAO` (Alternate interior angles)

So,
`\Delta CDO\sim \Delta ABO` according to Angle-Angle similarity.

Therefore, the ratio of corresponding sides will be same.

`\Rightarrow (OD)/(OB)=(OC)/(OA)`

`\Rightarrow (OD)/(OB)=(OC)/(3\cdot OC)`

`\Rightarrow (OD)/(OB)=(1)/(3)`

`\Rightarrow OB=3\cdot OD`