Question

A cylinder has a volume of 320 pi cu. in. and a height of 5". Find the radius of the cylinder. ...?

Answer 1

The volume of a cylinder can be calculated by the product of the area of the base times the height of the shape. It is expressed as follows:

V = πr²h

We calculate as follows:

320π in³= π (r²) (5 in)
64 in² = r²
r = 8 in

Hope this answers the question. Have a nice day.

Answer 2

radius of the cylinder is, 8 inches

Explanation:

Volume of cylinder(V) is given by:

`V = \pi r^2h` .....[1]

where,

r is the radius of the cylinder and

h is the height of the cylinder.

As per the statement:

A cylinder has a volume of 320 pi cu. in. and a height of 5"

⇒
`V = 320 \pi` cubic inches and h = 5 inches

Substitute these values in [1] we have

`320 \pi = \pi r^2 \cdot 5`

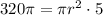
Simplify:

`320 = r^2 \cdot 5`

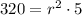
Divide both sides by 5 we have;

`64=r^2`

or

`r^2 = 64`

⇒
`r = √(64) = 8 in`

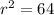
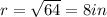
Therefore, the radius of the cylinder is, 8 inches