Question

Factor completely 50a2b5 – 35a4b3 + 5a3b4

Answer
10b2 – 7a2 + ab
a2b3(50b2 – 35a2 + 5ab)
5(10a2b5 – 7a4b3 + a3b4)
5a2b3(10b2 – 7a2 + ab)
...?

Answer 1

given expression is
`5a^(2) b^(3) (10b^(2)-7a^(2) +ab)`

Explanation:

Answer 2

The factored form of the given expression is
`5a^2b^3(10b^2-7a^2+ab)`

Explanation:

We have been given the expression
`50a^2b^5-35a^4b^3+5a^3b^4`

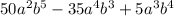
In order to factor it completely we can check for the GCF (greatest common factor) among all the three terms

The GCF is
`5a^2b^3`

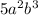
On factor out the GCF, we are left with

`5a^2b^3(10b^2-7a^2+ab)`

Therefore, the factored form of the given expression is
`5a^2b^3(10b^2-7a^2+ab)`