Answer:
yes, When the function
 is divided by x+10 , the remainder is zero.Therefore, x+10 is a factor of
is divided by x+10 , the remainder is zero.Therefore, x+10 is a factor of

Explanation:
We are given that

We have to find
 is a factor of given function.
is a factor of given function.
By remainder theorem
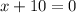
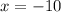
Substitute x=-10
Then , we get
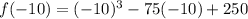
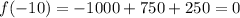
Remainder=f(-10)=0
It means x+10 is factor of given function f(x) because when x+10 divides the f(x) then we get remainder=0.
Answer:yes, When the function
 is divided by x+10 , the remainder is zero.Therefore, x+10 is a factor of
is divided by x+10 , the remainder is zero.Therefore, x+10 is a factor of
