Question

Find the distance between two points ( -1,1) and (2,-4)

Answer 1

The distance between two points ( -1,1) and (2,-4) is:

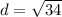`d=√(34)` or d = 5.8 units.

Explanation:

Given the points

• (-1, 1)

• (2, -4)

Finding the distance between (-1, 1) and (2, -4) using the formula

`d=√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

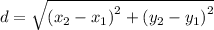
substitute (x₁, y₁) = (-1, 1) and (x₂, y₂) = (2, -4)

`=√(\left(2-\left(-1\right)\right)^2+\left(-4-1\right)^2)`

`=√(\left(2+1\right)^2+\left(-4-1\right)^2)`

`=√(3^2+5^2)`

`=√(9+25)`

`=√(34)` units

or

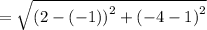
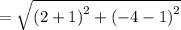
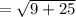
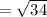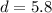`d = 5.8` units

Therefore, the distance between two points ( -1,1) and (2,-4) is:

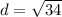`d=√(34)` or d = 5.8 units.