Question

What is a possible factorization of a polynomial with −5, 3, and i as zeros?

Answer 1

The zeros of the polynomial are: -5, 3 and i.

The zeros are the x-values that make each factor equal to zero, then if -5 is a zero:

`\begin{gathered} x=-5 \\ \text{Add 5 to both sides:} \\ x+5=-5+5 \\ x+5=0 \end{gathered}`

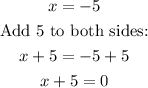
then (x+5) is one of the factors.

Zero: 3, thus:

`\begin{gathered} x=3 \\ \text{Subtract 3 from both sides} \\ x-3=3-3 \\ x-3=0 \\ (x-3)\text{ is another factor} \end{gathered}`

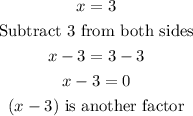
Zero: i, thus:

`\begin{gathered} x=i \\ \text{Subtract i from both sides} \\ x-i=i-i \\ x-i=0 \\ (x-i)\text{ is the last factor} \end{gathered}`

A possible factorization of the polynomial is: (x+5)(x-3)(x-i)